Operasi-operasi aritmetik untuk nombor, seperti penambahan, penolakan, pendaraban dan pembahagian, dibuat lebih umum dalam cabang matematik yang dikenali sebagai algebra niskala. Algebra niskala ialah kajian tentang sistem-sistem nombor abstrak, seperti kumpulan, gelanggang dan medan.
Jenis nombor
Nombor boleh dikelaskan kepada set yang dipanggil sistem nombor. Untuk kaedah-kaedah menyatakan nombor dengan simbol, sila lihat sistem angka.
Nombor asli
Nombor-nombor yang paling biasa digunakan ialah nombor asli. Bagi sesetengah orang, nombor asli bermaksud integer bukan negatif, manakala untuk orang yang lain, istilah itu bermakna integer positif. Integer-integer bukan negatif dirujuk sebagai nombor bulat, manakala integer positif dirujuk sebagai nombor pembilang.Dalam sistem penomboran asas sepuluh yang digunakan di hampir seluruh dunia, simbol-simbol untuk nombor asli ditulis dengan menggunakan sepuluh digit, iaitu 0 hingga 9. Suatu sistem nilai tempat tersirat yang bertambah dengan kuasa sepuluh digunakan untuk nombor yang lebih besar daripada sembilan. Oleh itu, nombor yang lebih besar daripada sembilan mempunyai angka yang dibentuk daripada dua or lebih digit. Simbol untuk set yang merangkumi semua nombor asli ialah
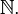
Integer
Nombor negatif ialah nombor yang nilainya adalah kurang daripada sifar. Nombor ini biasa ditulis dengan menggunakan tanda negatif di hadapan nombor positif yang sepadan untuk menandakan lawannya. Umpamanya, jika satu nombor positif digunakan untuk menandakan jarak di sebelah kanan titik tetap, nombor negatif akan digunakan untuk menandakan jarak di sebelah kiri. Serupa juga, jika satu nombor positif menandakan simpanan bank, jadi nombor negatif merujuk kepada pengeluaran wang daripada akaun bank itu. Apabila nombor bulatinteger (bahasa Jerman: Zahl, bentuk jamak Zahlen). negatif dicantumkan dengan nombor bulat positif atau nombor sifar, seseorang akan mendapat
(bahasa Jerman: Zahl, bentuk jamak Zahlen). negatif dicantumkan dengan nombor bulat positif atau nombor sifar, seseorang akan mendapat Nombor nisbah
Nombor nisbah ialah nombor yang boleh diungkapkan sebagai pecahan yang terdiri daripada pengangka integer serta penyebut nombor asli yang bukan sifar. Pecahan mewakili kuantiti yang diperoleh apabila sesuatu benda dibahagikan kepada
mewakili kuantiti yang diperoleh apabila sesuatu benda dibahagikan kepada 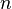 bahagian yang sama. Dua pecahan yang berbeza boleh mempunyai nilai yang sama dengan satu nombor nisbah; umpamanya
bahagian yang sama. Dua pecahan yang berbeza boleh mempunyai nilai yang sama dengan satu nombor nisbah; umpamanya  dan
dan  adalah sama. Jika nilai mutlak untuk
adalah sama. Jika nilai mutlak untuk  adalah lebih besar daripada
adalah lebih besar daripada 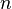 ,
nilai mutlak untuk pecahan itu adalah lebih besar daripada satu.
Pecahan boleh mempunyai nilai positif, negatif, atau sifar. Set untuk
semua pecahan merangkumi semua integer kerana setiap integer boleh
ditulis sebagai satu pecahan dengan penyebut 1. Simbol untuk nombor
nisbah ialah huruf tebal
,
nilai mutlak untuk pecahan itu adalah lebih besar daripada satu.
Pecahan boleh mempunyai nilai positif, negatif, atau sifar. Set untuk
semua pecahan merangkumi semua integer kerana setiap integer boleh
ditulis sebagai satu pecahan dengan penyebut 1. Simbol untuk nombor
nisbah ialah huruf tebal 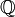 (untuk quotient dalam bahasa Inggeris, iaitu hasil bahagi).
(untuk quotient dalam bahasa Inggeris, iaitu hasil bahagi).Nombor nyata
Dengan kurang tepat, nombor-nombor nyata boleh dianggap sebagai sama sahaja dengan titik-titik pada garis selanjar. Semua nombor nisbahadalah nombor nyata dan seperti dengan nombor nisbah, nombor nyata boleh dikelaskan, baik sebagai positif, sifar, mahupun negatif. Nombor nyata boleh dicirikan dengan unik melalui sifat matematiknya: nombor ini adalah medan tertib lengkap yang tunggal. Bagaimanapun, nombor nyata bukannya suatu medan tertutup algebra.Angka-angka perpuluhan adalah lagi satu cara untuk mengungkapkan nombor. Dalam sistem nombor asas sepuluh, nombor ini ditulis sebagai rentetan angka, dengan satu titik (titik perpuluhan) (umpamanya di Amerika Syarikat dan United Kingdom) atau dengan satu koma (umpamanya di benua Eropah) di sebelah kanan tempat nilai-nilai satu; nombor nyata negatif ditulis dengan tanda minus di hadapan. Sesuatu angka perpuluhan yang mentakrifkan nombor rasional boleh berulang-ulang atau tamat (walaupun seberapa banyak nombor sifar boleh ditambah), walaupun sifar ialah nombor nyata yang tunggal yang tidak boleh ditakrifkan melalui angka perpuluhan yang berulang-ulang. Umpamanya, pecahan
 boleh ditulis sebagai angka perpuluhan 1.25 yang tamat, atau sebagai
angka perpuluhan 1.24999... (angka-angka sembilan yang berterusan) yang
berulang-ulang. Pecahan
boleh ditulis sebagai angka perpuluhan 1.25 yang tamat, atau sebagai
angka perpuluhan 1.24999... (angka-angka sembilan yang berterusan) yang
berulang-ulang. Pecahan  hanya boleh ditulis dengan 0.3333... (angka-angka tiga yang
berterusan) yang berulang-ulang. Semua angka perpuluhan yang
berulang-ulang atau tamat mentakrifkan nombor nyata yang juga boleh
ditulis sebagai pecahan; 1.25 =
hanya boleh ditulis dengan 0.3333... (angka-angka tiga yang
berterusan) yang berulang-ulang. Semua angka perpuluhan yang
berulang-ulang atau tamat mentakrifkan nombor nyata yang juga boleh
ditulis sebagai pecahan; 1.25 =  dan 0.3333... =
dan 0.3333... =  . Sebaliknya, angka-angka yang tidak berulang-ulang atau tidak tamat mewakili nombor bukan nisbah, iaitu nombor-nombor yang tidak boleh ditulis sebagai pecahan. Umpamanya pemalar-pemalar matematik yang terkenal seperti π (pi) dan
. Sebaliknya, angka-angka yang tidak berulang-ulang atau tidak tamat mewakili nombor bukan nisbah, iaitu nombor-nombor yang tidak boleh ditulis sebagai pecahan. Umpamanya pemalar-pemalar matematik yang terkenal seperti π (pi) dan  , punca kuasa dua 2,
adalah nisbah; serupa juga dengan nombor nyata yang diungkapkan oleh
angka perpuluhan 0.101001000100001... kerana ungkapan ini tidak berulang
atau tamat.
, punca kuasa dua 2,
adalah nisbah; serupa juga dengan nombor nyata yang diungkapkan oleh
angka perpuluhan 0.101001000100001... kerana ungkapan ini tidak berulang
atau tamat.Nombor-nombor nyata terdiri daripada semua nombor yang boleh diungkapkan melalui angka perpuluhan, baik nombor nisbah mahupun nisbah. Simbol untuk nombor nyata ialah
 ukuran, dan adalah sama dengan titik-titik pada garis nombor. Oleh sebab ukuran-ukuran hanya dibuat pada tahap ketepatanjidar selisih selalu wujud apabila nombor nyata digunakan untuk mewakilinya. Ini sering diolahkan dengan menentukan bilangan angka bererti yang sesuai. Nombor-nombor nyata telah dipergunakan untuk mewakili yang tertentu,
ukuran, dan adalah sama dengan titik-titik pada garis nombor. Oleh sebab ukuran-ukuran hanya dibuat pada tahap ketepatanjidar selisih selalu wujud apabila nombor nyata digunakan untuk mewakilinya. Ini sering diolahkan dengan menentukan bilangan angka bererti yang sesuai. Nombor-nombor nyata telah dipergunakan untuk mewakili yang tertentu, Nombor kompleks
Beralih ke tahap pengabstrakan yang lebih tinggi, nombor-nombor nyata boleh diperluas supaya merangkumi nombor-nombor kompleks Dari segi sejarah, set nombor muncul daripada soalan bolehkah nombor negatif mempunyai punca kuasa dua. Daripada masalah ini, satu nombor baru telah ditemui: punca kuasa dua negatif satu. Nombor ini ditandakan dengan simbol
Dari segi sejarah, set nombor muncul daripada soalan bolehkah nombor negatif mempunyai punca kuasa dua. Daripada masalah ini, satu nombor baru telah ditemui: punca kuasa dua negatif satu. Nombor ini ditandakan dengan simbol  yang diberikan oleh Leonhard Euler.
yang diberikan oleh Leonhard Euler.Nombor-nombor kompleks terdiri daripada semua nombor dengan bentuk
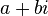 , dengan
, dengan 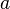 dan
dan  merupakan nombor-nombor nyata. Jika
merupakan nombor-nombor nyata. Jika 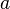 ialah sifar, maka
ialah sifar, maka 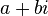 dipanggil nombor khayalan. Serupa juga, jika
dipanggil nombor khayalan. Serupa juga, jika  ialah sifar, maka
ialah sifar, maka 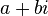 ialah nombor nyata kerana tidak adanya komponen khayalan. Sesuatu nombor kompleks yang mempunyai
ialah nombor nyata kerana tidak adanya komponen khayalan. Sesuatu nombor kompleks yang mempunyai 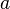 dan
dan  sebagai integer dipanggil integer Gaussan. Nombor-nombor kompleks merupakan medan tertutup algebra,
iaitu setiap polinomial dengan koefisien kompleks boleh difaktorkan
menjadi faktor-faktor linear yang mempunyai koefisien-koefisien
kompleks. Nombor-nombor kompleks adalah sepadan dengan titik-titik pada satah kompleks.
sebagai integer dipanggil integer Gaussan. Nombor-nombor kompleks merupakan medan tertutup algebra,
iaitu setiap polinomial dengan koefisien kompleks boleh difaktorkan
menjadi faktor-faktor linear yang mempunyai koefisien-koefisien
kompleks. Nombor-nombor kompleks adalah sepadan dengan titik-titik pada satah kompleks.Setiap sistem nombor yang disebut di atas adalah subset bagi sistem nombor yang berikut. Secara simbol, ini diwakili sebagai:

Angka
Nombor-nombor harus dibezakan daripada angka yang merupakan simbol untuk mewakili nombor. Nombor 'lima' boleh diwakili dengan kedua-dua angka asas sepuluh, iaitu 5, atau angka Roman, V. Notasi-notasi yang digunakan untuk mewakili nombor dibincangkan dalam rencana sistem angka yang berasingkan. Satu perkembangan yang penting dalam sejarah angka ialah perkembangan satu sistem tempat dan serupa dengan sistem perpuluhan moden, dapat mewakili nombor-nombor yang amat besar. Sebaliknya, angka-angka Roman memerlukan simbol-simbol tambahan untuk mewakili nombor-nombor yang lebih besar.
Sejarah
Sejarah integer
Nombor pertama
Maklumat selanjutnya: Sistem angka#Sejarah
Penggunaan nombor buat pertama kali yang diketahui bertarikh sejak sekitar 30000 SM, ketika gundal digunakan oleh orang-orang Paleolitik. Contoh terawal yang dikenali ialah dari sebuah gua di bahagian selatan Afrika. [1]. Sistem ini tidak mempunyai konsep nilai tempat (seperti dalam notasi perpuluhan yang digunakan sekarang) dan oleh itu, mengehadkan perwakilan nombor yang besar. Sistem pertama yang diketahui mempunyai nilai tempat ialah sistem asas 60 Mesopotamia (k.k. 3400 SM), dan sistem asas 10 terawal yang dikenali wujud sejak 3100 SMMesir. [2] di
Sejarah sifar
Maklumat selanjutnya: 0 (nombor)#Sejarah
Penggunaan sifar sebagai satu nombor harus dibezakan daripada penggunaannya sebagai satu angka pemegang tempat dalam sistem-sistem nilai tempat. Banyak teks India kuno menggunakan perkataan Sanskrit shunya untuk merujuk kepada konsep lowong; dalam teks matematik, perkataan ini sering digunakan untuk merujuk kepada nombor sifar. [3]. Dengan cara yang sama, Pāṇini (abad ke-5 SM) menggunakan pengoperasi nol (sifar, iaitu penerbitan lambda) dalam tatabahasa algebranya, Ashtadhyayi, untuk bahasa Sanskrit (lihat juga Pingala)
Rekod-rekod menunjukkan bahawa orang-orang Yunani kelihatan tidak pasti tentang status sifar sebagai satu nombor: mereka tertanya-tanya tentang "bagaimana 'tidak ada apa-apa' boleh merupakan sesuatu?", dan menimbulkan perdebatan falsafah dan menjelang Zaman Pertengahan, juga perdebatan agama yang menarik tentang sifat dan kewujudan sifar serta hampagas. Paradoks Zeno dari Elea bergantung sebahagian besar kepada tafsiran sifar yang tidak pasti. (Orang-orang Yunani juga mempersoalkan tentang adakah 1 merupakan salah satu nombor.)
Orang-orang Olmec dari Mexico tengah selatan yang lebih lewat memulakan penggunaan sifar benar di dalam Dunia Baru, mungkin sejak abad ke-4 SM tetapi pasti pada 40 SM. Sifar benar itu dijadikan oleh mereka sebagai satu angka yang perlu untuk angka-angka Maya dan takwim Maya, tetapi penggunaan mereka ini tidak mempengaruhi sistem-sistem angka Dunia Lama.
Menjelang tahun 130 Masihi, Ptolemy yang dipengaruhi oleh Hipparchus dan orang-orang Babylon, menggunakan satu simbol untuk sifar (satu bulatan kecil dengan satu palang yang panjang di atasnya) yang sebelum itu, menggunakan abjad dalam sistem angka perenampuluhan. Disebabkan nombor sifar ini digunakan secara berasingan, dan bukan sahaja sebagai pemegang tempat, sifar keyunanian ini merupakan penggunaan sifar benar yang 'didokumenkan' buat pertama kali di dalam Dunia Lama. Untuk manuskrip-manuskrip Rom Timur yang kemudian bagi karynanya, Syntaxis Mathematica (Almagest), bentuk sifar keyunanian Ptolemy telah diubah menjadi huruf Greek, omikron (sebelum itu bermaksud 70).
Menjelang tahun 525 Masihi, lagi satu sifar benar telah digunakan di dalam jadual-jadual, bersama-sama dengan angka Rom (penggunaan pertama yang diketahui adalah oleh Dionysius Exiguus), tetapi sebagai perkataan, iaitu nulla yang bermaksud tidak ada satu pun, dan bukannya sebagai satu simbol. Apabila pembahagian menghasilkan sifar sebagai bakinya, nihiltiada ada satu pun, digunakan. Sifar-sifar Zaman Pertengahan ini digunakan oleh semua komputus (penghitung Easter) Zaman Pertengahan yang kemudian. Pada sekitar 725 Masihi, parap N telah digunakan di dalam jadual angka Rom oleh Bede, atau teman sekerjanya, dan merupakan satu penggunaan terasing, serta satu simbol sifar yang benar. yang juga bermaksud
Satu penggunaan sifar yang awal oleh Brahmagupta yang telah didokumenkan di dalam Brahmasphutasiddhanta bertarikh sejak tahun 628 Masihi. Beliau mengolahkan sifar sebagai satu nombor, dan membincangkan operasi-operasi yang melibatkannya, termasuk pembahagian. Pada masa ini, iaitu abad ke-7, konsep ini jelas telah tiba di Kemboja, dan dokumen-dokumen menunjukkan bahawa idea ini kemudian tersebar ke China dan dunia Islam.
Sejarah nombor negatif
Maklumat selanjutnya: Nombor negatif dan bukan negatif#Penggunaan pertama nombor negatif
Konsep abstrak bagi nombor-nombor negatif telah diakui seawal 100 - 50 SM. Karya Cina, "Sembilan Bab mengenai Seni Matematik" (Jiu-zhang Suanshu) mengandungi kaedah-kaedah untuk menentukan keluasan gambar rajah; palang merah digunakan untuk menandakan pekalidunia Timur; rujukan pertama dalam karya Barat adalah pada abad ke-3Greece. Diophantus merujuk kepada persamaan
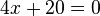 (penyelesaiannya adalah negatif) di dalam karyanya, Arithmetica, dan mengatakan bahawa persamaan itu memberikan hasil bukan-bukan. positif, dan palang hitam untuk pekali negatif. Ini merupakan sebutan nombor negatif yang pertama diketahui di di
(penyelesaiannya adalah negatif) di dalam karyanya, Arithmetica, dan mengatakan bahawa persamaan itu memberikan hasil bukan-bukan. positif, dan palang hitam untuk pekali negatif. Ini merupakan sebutan nombor negatif yang pertama diketahui di di Semasa dekad 600-an, nombor-nombor negatif telah digunakan di India untuk mewakili hutang. Rujukan-rujukan Diophantus dahulu telah dibincangkan dengan lebih ketara oleh Brahmagupta, ahli matematik India, di dalam karyanya Brahma-Sphuta-Siddhanta pada tahun 628 Masihi. Beliau menggunakan nombor-nombor negatif untuk menghasilkan rumus kuadratik, satu bentuk am yang masih digunakan pada hari ini. Bagaimanapun pada abad ke-12 di India, Bhaskara memberikan punca kuasa negatif untuk persamaan-persamaan kuadratik, tetapi berkata bahawa nilai negatif "dalam kes ini tidak diambil kerana tidak sempurna; orang-orang tidak akan bersetuju dengan punca-punca kuasa negatif."
Ahli-ahli matematik Eropah biasanya menahan konsep nombor-nombor negatif sehingga abad ke-17, walaupun Fibonacci membenarkan penyelesaian negatif yang ditafsirkannya sebagai debit (bab 13 daripada Liber Abaci, 1202) dan kemudiannya sebagai kerugian (dalam Flos). Pada waktu yang sama, orang-orang Cina menandakan nombor-nombor negatif melalui satu coret serong pada digit bukan sifar yang paling kanan untuk angka nombor positif yang sepadan. Penggunaan pertama nombor negatif dalam karya Eropah adalah oleh Chuquet pada abad ke-15. Beliau menggunakannya sebagai eksponen, tetapi merujuk kepadanya sebagai "nombor bukan-bukan"
Baru-baru pada abad ke-18, ahli mathematik Switzerland, Leonhard Euler, mempercayai bahawa nombor negatif adalah lebih besar berbanding dengan ketakterhinggaan. Adalah amalan biasa pada masa itu untuk tidak mengendahkan sebarang hasil negatif yang dikembalikan oleh persamaan, berdasarkan andaian bahawa angka-angka itu tidak bermakna.
Sejarah nombor rasional, nisbah, dan nombor nyata
Maklumat selanjutnya: Sejarah nisbah dan Sejarah pi
Sejarah nombor rasional
Konsep nombor-nombor pecahan mungkin wujud sejak zaman prasejarah. Orang-orang Mesir Kuno juga menulis teks matematik yang memerihalkan bagaimana mengubahkan pecahannotasi khas. Ahli matematik Greek klasik dan India mengkaji teori nombor rasional sebagai sebahagian kajian am untuk teori nombor. Kajian yang paling terkenal ialah Unsur-unsur Euclid yang wujud sejak kira-kira 300 SM. Antara teks-teks India, kajian yang paling berkait ialah Sutra Sthananga yang juga merangkumi teori nombor sebagai sebahagian kajian am matematik. menjadiKonsep pecahan perpuluhan amat berkait dengan notasi nilai tempat perpuluhan; kedua-dua ini nampaknya berkembang bersama-sama. Umpamanya, sutra-sutra matematik Jain biasanya termasuk penghitungan penghampiran pecahan perpuluhan untuk pi atau punca kuasa dua untuk dua. Serupa juga, teks-teks matematik Babylon selalu menggunakan pecahan-pecahan perenam-puluhan dengan amat kerap.
Sejarah nisbah
Penggunaan nombor tak nisbah terawal yang diketahui terdapat dalam Sulba Sutra India yang dikarang sekitar 800-500 SM. Bukti kewujudan terawal nombor tak nisbah dipercayai berpunca daripada Pythagoras, atau secara lebih khususnya pengiktu beliau Hippasus dari Metapontum, yang menghasilkan bukti (paling mungkin secara geometri) ketaknisbahan punca kuasa dua dari 2. Mengikut kisah, Hippasus menemui nonbor tak nisbah ketika cuba menggambarkan punca kuasa dua 2 sebagai satu pecahan. Namun, Pythagoras percaya akan kemutlakan nombor, dan tidak dapat menerima kewujudan nombor tak nisbah. Beliau tidak mampu membuktikan ketidakwujudannya melalui logik, namun kepercayaan beliau tidak mampu menerima kewujudan nombor tak nisbah maka beliau menghukum mati Hippasus dengan melemaskannya.Abad ke-16 melihatkan penerimaan muktamad nombor negatif, integer dan pecahan oleh orang Eropah. Abad ke-17 melihatkan pecahan perpuluhan dengan notasi moden digunakan secara meluas oleh ahli matematik. Namun, hanya ketika abad-19 barulah nombor tak nisbah dibahagi kepada bahagian algebra dan transendental, dan satu kajian saintifik mengenai teori monbor tak nisbah timbul lagi setelah lama terpendam sejak zaman Euclid. Tahun 1872 menyaksikan penerbitan teori-teori Karl Weierstrass (oleh anak muridnya Kossak), Heine (Crelle, 74), Georg Cantor (Annalen, 5), dan Richard Dedekind. Pada tahun 1869 kajian Méray menyimpang dari titik yang serupa dengan Heine, namun teori itu dirujuk secara amnya kepada tahun 1872. Keadah Weierstrass telah dikemukakan sepenuhnya oleh Pincherle (1880), dan kadeah Dedekind pula menerima makin menonjol melalui kerja-kerja lanjutan pengarang tersebut (1888) dan disusuli dukungan oleh Paul Tannery (1894). Weierstrass, Cantor, dan Heine mengasaskan teori masing-masing pada siri tak terhingga, manakala Dedekind mengasaskan teori beliau pada idea potongan (Schnitt) dalam sistem nombor nyata, maka memisahkan semua nombor nisbah kepada dua kumpulan yang melihatkan ciri-ciri biasa yang tertentu. Subjek ini kemudiannya menerima sumbangan lanjut di tangan Weierstrass, Kronecker (Crelle, 101), dan Méray.
Pecahan berlanjar yang berkait rapat dengan nombor tak nisbah (dan oleh sebab Cataldi, 1613), menarik perhatian di tangan Euler, dan pada awal abad ke-19 pula ditonjolkan melalui penulisan Joseph Louis Lagrange. Sumbangan penting lain turut dilakukan oleh Druckenmüller (1837), Kunze (1857), Lemke (1870), dan Günther (1872). Ramus (1855) mula-mula menghubungkaitkan subjek ini dengan penentu, mencetuskan sumbangan seterusnya oleh Heine, Möbius, dan Günther, dalam teori Kettenbruchdeterminanten. Dirichlet juga menokok tambah teori amnya, seperti mana yang dilakukan ramai penyumbang kepada aplikasi subjek ini.
Nombor transenden dan nombor nyata
Hasil kajian terulung mengenai nombor transenden merupakan bukti yang dikemukakan oleh Johann Heinrich Lambert pada tahun 1761 bahawa π tidak boleh berbentuk nombor nisbah, dan juga bahawa en tidak nisbah jika n nisbah (melainkan n = 0). (Pemalar e pertama kali disentuh dalam kerja John Napier tahun 1618 mengenai logaritma.) Legendre memperkuatkan bukti ini untuk menunjukkan bahawa π bukan kuasa dua kepada suatu nombor nisbah. Pencarian kuasa persamaan kuintik dan berdarjah lebih tinggi merupakan perkembangan penting, teorem Abel–Ruffini (Ruffini 1799, Abel 1824) menunjukkan bahawa ini tidak boleh diselesaikan dengan radikal (formula yang hanya melibatkan operasi dan punca aritmatik). Maka, adalah perlu untuk mengambil kira set nombor algebra yang lebih luas (segala penyelesaian kepada persamaan-persamaan polinomial). Évariste Galois (1832) mengaitkan persamaan-persamaan polinomial kepada teori kelompok yang membangkitkan bidang teori Galois.Set nombor algebra pun tidak mencukupi dan set penuh nombor nyata termasuklah nombor transenden, yang kewujudannya dibutkikan puat julung kalinya oleh Joseph Liouville (1844, 1851). Pada tahun 1873, Charles Hermite membuktikan bahawa e adalah nombor transenden dan pada tahun 1882, Ferdinand von Lindemann membuktikan bahawa π juga transenden. Akhirnya Cantor menunjukkan bahawa set segala nombor nyata adalah tidak berkira dan tidak terhingga tetapi set segala nombor algebra adalah tidak terhingga tetapi berkira, maka terdapatlah bilangan nombor transenden yang tidak berkira dan tidak terhingga.
Ketakterhinggaan
Maklumat selanjutnya: Sejarah ketakterhinggaan
Tanggapan terawal yang diketahui mengenai ketakterhinggaan matematik muncul di dalam Veda Yajur yang pada sebahagiannya menyatakan: "jika anda mengeluarkan sebahagian daripada ketakterhinggaan atau menambah sebahagian kepadanya, hasilnya masih merupakan ketakterhinggaan". Ketakterhinggaan merupakan satu topik kajian falsafah yang popular antara ahli-ahli matematik Jain pada kira-kira 400 SM. Mereka membezakan antara lima jenis ketakterhinggaan: tak terhingga pada satu atau dua arah, keluasan yang tak terhingga, ketakterhinggaan pada mana-mana satu arah, dan ketakterhinggan sepanjang masa.
Di dunia Barat, tanggapan tradisional mengenai ketakterhinggaan matematik ditakrifkan oleh Aristotle yang membezakan ketakterhinggaan sebenar dan ketakterhinggaan berpotensi; sepersetujuan yang dicapai adalah bahawa hanya ketakterhinggaan berpotensi mempunyai nilai benar. Karya Galileo, Dua Sains Baru, membincangkan idea kesepadanan satu ke satu antara set-set tak terhingga. Bagaimanapun, kemajuan utama yang berikutnya dibuat oleh Georg Cantor pada tahun 1895 apabila beliau menerbitkan sebuah buku mengenai teori set yang baru, dan memperkenalkan hipotesis kontinum, antara lain.
Versi geometri moden untuk ketakterhinggaan diberikan oleh geometri unjuran yang memperkenalkan "titik-titik unggul pada ketakterhinggaan," dengan satu titik bagi setiap arah ruang. Setiap keluarga garis-garis selari pada satu arah yang tertentu dipostulatkan akan bertemu di titik unggul yang sepadan. Ini amat berkait dengan idea titik-titik lenyap di dalam lukisan perspektif.
Nombor kompleks
Maklumat selanjutnya: Nombor kompleks#Sejarah
Sentuhan sepintas lalu yang terawal mengenai punca kuasa dua nombor negatif didapati dalam kerja ahli matematik dan pencipta Greek, Heron dari Alexandria, pada abad pertama M, apabila beliau mengambil kira isi padu sesuatu frustum mustahil dalam piramid. Perihal punca kuasa dua nombor negatif ini menonjol pada abad ke-16 apabila formula-formula tertutup untuk punca-punca polinomial darjah ketiga dan keempat ditemui oleh ahli matematik Itali (lihat Niccolo Fontana Tartaglia, Gerolamo Cardano). Tidak lama kemudian, adalah didapati bahawa formula-formula ini, sungguhpun jika seseorang itu hanya berminat terhadap penyelesaian nyata, namun kadang-kala memerlukan manipulasi punca kuasa dua nombor negatif.
Inipun makin membingungkan kerana mereka tidak pun mengamil kira nombor negatif dengan dasar yang kuat pada masa itu. Istilah "hayalan" bagi kuantiti-kuantiti ini dicadangkan oleh René Descartes pada tahun 1637 dan sepatutnya membawa erti penghinaan (lihat nombor hayalan bagi membincangkan "realiti" nombor kompleks). Satu lagi sumber kekeliruan ini adalah bahawa persamaan
 kelihatan tidak konsisten dan tidak menentu dengan identiti algebra
kelihatan tidak konsisten dan tidak menentu dengan identiti algebra  yang sah untuk nombor nyata positif a dan b, serta juga digunakan dalam pengiraan nombor kompleks dengan mana-mana antara a, b positif dan nombor negatif yang lain. Penyalahgunaan identiti ini (dan identiti
yang sah untuk nombor nyata positif a dan b, serta juga digunakan dalam pengiraan nombor kompleks dengan mana-mana antara a, b positif dan nombor negatif yang lain. Penyalahgunaan identiti ini (dan identiti  yang berkaitan) yang mana kedua-dua a dan b adalah engatif pun membingungkan Euler. Kesulitan ini kemudiannya membawa beliau kepada kelaziman menggunakan simbol khas i untuk menggantikan
yang berkaitan) yang mana kedua-dua a dan b adalah engatif pun membingungkan Euler. Kesulitan ini kemudiannya membawa beliau kepada kelaziman menggunakan simbol khas i untuk menggantikan 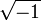 untuk mencegah kesilapan ini.
untuk mencegah kesilapan ini.Abad ke-18 melihatkan titik peluh Abraham de Moivre dan Leonhard Euler. De Moivre (1730) dihargai dengan formula terkenal yang dinamakan bersempena beliau, iaitu formula de Moivre:
Juga pada tahun 1799, Gauss mengemukakan bukti diterima umum pertama bagi teorem asas algebra, untuk menunjukkan bahawa setiap polinomial pada nombor kompleks mempunyai set penuh penyelesaian dalam bidang ini. Penerimaan umum teori nombor kompleks ini tidak sedikit pun merupakan hasil Augustin Louis Cauchy dan Niels Henrik Abel, khususnya Abel yang merupakan yang pertama untuk berani menggunakan nombor kompleks lalu mencapai kejayaan yang terkenal.
Gauss mengkaji nombor-nombor kompleks bagi bentuk
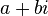 , yang mana a dan b adalah integer atau nisbah (dan i ialah salah satu daripada dua punca
, yang mana a dan b adalah integer atau nisbah (dan i ialah salah satu daripada dua punca  ). Anak muridnya, Ferdinand Eisenstein, mengkaji
). Anak muridnya, Ferdinand Eisenstein, mengkaji 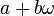 , yang mana
, yang mana  ialah punca kompleks bagi
ialah punca kompleks bagi  . Kelas-kelas nombor kompleks sedemikian yang lain (iaitu medan siklotomik) berasal daripada punca kesean
. Kelas-kelas nombor kompleks sedemikian yang lain (iaitu medan siklotomik) berasal daripada punca kesean  bagi nilai-nilai
bagi nilai-nilai  yang lebih tinggi. Pengitlakan ini banyak berpunca daripada Kummer yang juga mencipta nombor unggul yang diungkapkan sebagai entiti geometri oleh Felix Klein pada tahun 1893. Teori am medan-medan ini direka oleh Évariste Galois yang mengkaji medan-medan yang dijana olej akar kepada mana-mana persamaan polinomial
yang lebih tinggi. Pengitlakan ini banyak berpunca daripada Kummer yang juga mencipta nombor unggul yang diungkapkan sebagai entiti geometri oleh Felix Klein pada tahun 1893. Teori am medan-medan ini direka oleh Évariste Galois yang mengkaji medan-medan yang dijana olej akar kepada mana-mana persamaan polinomialNombor perdana
Nombor-nombor perdana telah dikaji pada sepanjang sejarah tercatat. Euclid mengekhaskan sebuah buku dalam Unsur-unsurnya untuk teori nombor perdana; dalam buku itu, beliau membuktikan ketakterhinggaan nombor-nombor perdana serta teorem asas aritmetik, dan menyampaikan algoritma Euclid untuk memperoleh pembahagi sepunya terbesar untuk dua nombor.Pada tahun 240 SM, Eratosthenes menggunakan Saringan Eratosthenes untuk mengasingkan nombor-nombor perdana dengan cepat. Bagaimanapun, kebanyakan perkembangan lanjutan bagi teori nombor perdana di Eropah wujud sejak Zaman Pembaharuan Renaissance dan zaman-zaman kemudian.
Pada tahun 1796, Adrien-Marie Legendre menerka teorem nombor perdana, dan memerihalkan taburan asimptot untuk nombor-nombor perdana. Hasil-hasil lain mengenai taburan nombor perdana termasuk bukti Euler yang menyatakan bahawa hasil tambah untuk salingan-salingan mencapah, serta konjektur Goldbach yang mendakwa bahawa mana-mana satu nombor genap yang cukup besar adalah hasil tambah dua nombor perdana. Lagi satu konjektur yang berkaitan dengan taburan nombor-nombor perdana ialah hipotesis Riemann yang dirumuskan oleh Bernhard Riemann pada tahun 1859. Teorem nombor perdana akhirnya dibuktikan oleh Jacques Hadamard dan Charles de la Vallee-Poussin pada tahun 1896.
Sumber : http://ms.wikipedia.org/wiki/Nombor
![*[ NOTA PENGAJARAN DAN PEMBELAJARAN ]*](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiHxUHhLq34pRMpVRGwiF51pyvC7JJxHM4KP8Hd0-eys5qk5rcxSVddaZcsfy-aId0JdmPc3jv-cSpOIGYFhd63ImnzLHjMQMvzgMoZLw3ywNb7DyDlh0bX_KW-HsyU3dfbAtiQ4zygdxQ/s970/MATH+TEACHER+ONLINE+WITH+FRAME.jpg)


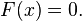
No comments:
Post a Comment