Introductions To Fractions

Fractions

A fraction is a part of a whole

Slice a pizza, and you will have fractions:

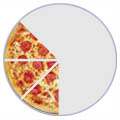1/2	1/4	3/8
(One-Half)	(One-Quarter)	(Three-Eighths)
The top number tells how many slices you have The bottom number tells how many slices the pizza was cut into.

Numerator / Denominator

We call the top number the Numerator, it is the number of parts you have.
We call the bottom number the Denominator, it is the number of parts the whole is divided into.

Numerator

Denominator

You just have to remember those names! (If you forget just think "Down"-ominator)

Equivalent Fractions

Some fractions may look different, but are really the same, for example:

4/8	=	2/4	=	1/2
(Four-Eighths)		Two-Quarters)		(One-Half)
	=		=

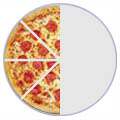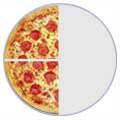It is usually best to show an answer using the simplest fraction ( ¹/₂ in this case ). That is called Simplifying, or Reducing the Fraction

Adding Fractions

You can add fractions easily if the bottom number (the denominator) is the same:

1/4	+	1/4	=	2/4	=	1/2
(One-Quarter)		(One-Quarter)		(Two-Quarters)		(One-Half)
	+		=		=

Another example:

5/8	+	1/8	=	6/8	=	3/4
	+		=		=

Adding Fractions with Different Denominators

But what if the denominators (the bottom numbers) are not the same? As in this example:

3/8	+	1/4	=	?
	+		=

You must somehow make the denominators the same.
In this case it is easy, because we know that ¹/₄ is the same as ²/₈ :

3/8	+	2/8	=	5/8
	+		=

In that example it was easy to make the denominators the same, but it can be harder ... so you may need to use either of these methods:

• Least Common Denominator, or
• Common Denominator

to make them the same (they both work, use whichever you prefer).

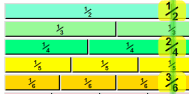
Equivalent Fractions

Equivalent Fractions have the same value, even though they may look different.

These fractions are really the same:

1 2

=

2 4

=

4 8

Why are they the same? Because when you multiply or divide both the top and bottom by the same number, the fraction keeps it's value.
The rule to remember is:

What you do to the top of the fraction
you must also do to the bottom of the fraction !

So, here is why those fractions are really the same:

	× 2		× 2
1	=	2	=	4
2		4		8
	× 2		× 2

And visually it looks like this:

1/2		2/4		4/8
	=		=

See the Animation See Fractions on the Number Line ... it shows you many equivalent fractions We also have a Chart of Fractions with many examples of equivalent fractions.

Dividing

Here are some more equivalent fractions, this time by dividing:

	÷ 3		÷ 6
18	=	6	=	1
36		12		2
	÷ 3		÷ 6

If we keep dividing until we can't go any further, then we have simplified the fraction (made it as simple as possible).

Important:

The top and bottom of the fraction must always be a whole number.
So, what you divide by must divide evenly (ie no remainders) for both the top and bottom numbers.
You only multiply or divide, never add or subtract, to get an equivalent fraction.

Simplifying Fractions

To simplify a fraction, divide the top and bottom by the highest number that
can divide into both numbers exactly.

Simplifying Fractions

Simplifying (or reducing) fractions means to make the fraction as simple as possible. Why say four-eighths (⁴/₈) when you really mean half (¹/₂) ?

	4/8	==>	2/4	==>	1/2
	(Four-Eighths)		(Two-Quarters)		(One-Half)

How do I Simplify a Fraction ?

There are two ways to simplify a fraction:

Method 1

Try dividing both the top and bottom of the fraction until you can't go any further (try dividing by 2,3,5,7,... etc).

Example: Simplify the fraction ²⁴/₁₀₈ :

	÷ 2		÷ 2		÷ 3
24	=	12	=	6	=	2
108		54		27		9
	÷ 2		÷ 2		÷ 3

Method 2

Divide both the top and bottom of the fraction by the Greatest Common Factor, (you have to work it out first!).

Example: Simplify the fraction ⁸/₁₂ :

1. The largest number that goes exactly into both 8 and 12 is 4, so the Greatest Common Factor is 4.

2. Divide both top and bottom by 4:

	÷ 4
8	=	2
12		3
	÷ 4

And the answer is: ²/₃

Fractions on the Number Line Also ... see an animation of Fractions on the Number Line where you can see many common fractions and their simpler version. We also have a chart of fractions with the simplest fraction highlighted.