Adding whole numbers

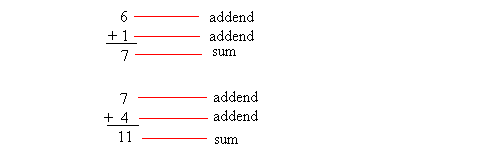
Adding whole numbers is what this lesson will teach you. Also there is a calculator to help you practice.Adding whole numbers means that we are combining numbers to form a total.
Each number being added is called an addend and the total, which is the answer to the addition problem is called sum.



Adding numbers with 1 digit is pretty straightforward. In general, you can do it mentally or use your fingers. Adding zero to a number never changes the number

Take a close look at the following addition problems.

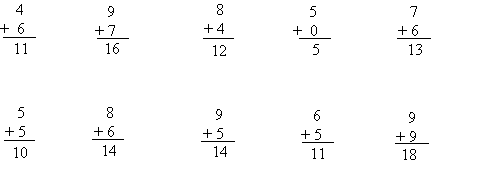
The answer for one of them is wrong. Can you tell which one?

You got it right! It is the first one. 4 + 6 is not equal to 11.

4 + 6 = 10.

Now, let us move on to something more interesting, adding numbers with two digits.

When adding two-digit numbers, add the ones first. Then, add the tens.

Let us try to add 36 to 17 using expanded notation

36 = 30 + 6 and 17 = 10 + 7

adding the ones ( 6 and 7) gives 13 and 13 = 10 + 3

Adding the tens (30, 10, and 10) gives 50 and 50 + 3 = 53


Let us add 58 to 46

58 = 50 + 8 and 46 = 40 + 6

Adding the ones (8 and 6 ) gives 14 and 14 = 10 + 4

Adding the tens (50, 40, and ,10) gives 100 and 100 + 4 = 104

We can accomplish the same by arranging the numbers in vertical columns as shown below

In the above, we add the ones column first. Then, we carry over the tens to the tens column. The 1 that we carry over has a place value of 10. However, there is no need to write 10 because as we saw before in place value putting a 1 here in the tens place means that there is 1 ten.

How to Add Faster Than a Calculator

Calculators are amazing gadgets that do all sorts of calculations. But you can't always find a calculator when you need one, and the occasional dead battery or limited light makes it impossible to operate one. Learn addition tricks that amaze your friends when you can add faster than a calculator can.

Instructions

1. o Remember that numbers are reversible in addition. For example, 33 + 567 is the same as 567 + 33. Always start with the largest number in order to count less and faster.
2. o Round off to the nearest multiple of ten when adding. Multiples of ten are significantly easier to manipulate than numerals that end in 7, 8 or 9. When you add 79 + 19, see both numbers as being one away from multiples of 10 or 80 + 20. You know that the answer to 80 + 20 is 100, so just subtract the 2 that you previously added to the numbers from the final answer.
3. o Use the place value of 10 as another way of adding faster when only one of your numbers is close to 10. For example, if you're adding 63 + 28, you know that 28 is just 2 less than 30. When you add 2 to 28 for 30, take 2 off your other number, 63 - 2 = 61. Then add 61 + 30 for an easier equation.
4. o Add the ones first. Numbers have place values: ones, tens, hundred, thousands and so on. When you add the ones first, it makes it easier to add on the next place value. Look at 335 + 112. Add the ones, 5 + 2 = 7. Add your ones to the result of the tens place value, in this case, 30 + 10. So far you have 47, and all you have left is to add them to the hundreds place value numbers, 300 + 100 = 400 + 47 = 447.