Division with Remainders
When we are given a long division to do it will not always work out to a whole number.
Sometimes there will be numbers left over. These are known as remainders.
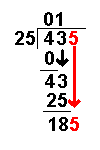
Taking an example similar to that on the Long Division page it becomes more clear:
435 ÷ 25
(If you feel happy with the process on the Long Division page you can skip the first bit.)
![*[ NOTA PENGAJARAN DAN PEMBELAJARAN ]*](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiHxUHhLq34pRMpVRGwiF51pyvC7JJxHM4KP8Hd0-eys5qk5rcxSVddaZcsfy-aId0JdmPc3jv-cSpOIGYFhd63ImnzLHjMQMvzgMoZLw3ywNb7DyDlh0bX_KW-HsyU3dfbAtiQ4zygdxQ/s970/MATH+TEACHER+ONLINE+WITH+FRAME.jpg)
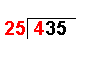
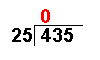
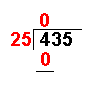
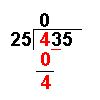
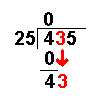
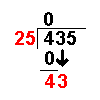
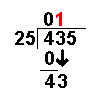
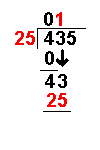
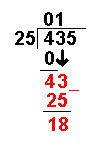
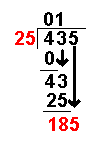
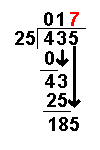
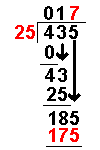
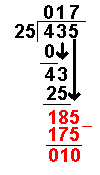
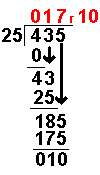
No comments:
Post a Comment